LDPC編譯碼原理
 發布時間:2021-07-01
閱讀量:47
分(fēn)享:
發布時間:2021-07-01
閱讀量:47
分(fēn)享:
https://blog.csdn.net/sinat_38151275/article/details/98102699
低密度校驗碼(LDPC碼)是一(yī)種前向糾錯碼,LDPC碼最早在20世紀60年代由Gallager在他的博士論文中(zhōng)提出,但限于當時的技術條件,缺乏可行的譯碼算法,此後的35年間基本上被人們忽略,其間由Tanner在1981年推廣了LDPC碼并給出了LDPC碼的圖表示,即後來所稱的Tanner圖。1993年Berrou等人發現了Turbo碼,在此基礎上,1995年前後MacKay和Neal等人對LDPC碼重新進行了研究,提出了可行的譯碼算法,從而進一(yī)步發現了LDPC碼所具有的良好性能,迅速引起強烈反響和極大(dà)關注。經過十幾年來的研究和發展,研究人員(yuán)在各方面都取得了突破性的進展,LDPC碼的相關技術也日趨成熟,甚至已經開(kāi)始有了商(shāng)業化的應用成果,并進入了無線通信等相關領域的标準。
LDPC碼的特點
LDPC碼是一(yī)種分(fēn)組碼,其校驗矩陣隻含有很少量非零元素。正是校驗矩陣的這種稀疏性,保證了譯碼複雜(zá)度和最小(xiǎo)碼距都隻随碼長呈現線性增加。除了校驗矩陣是稀疏矩陣外(wài),碼本身與任何其它的分(fēn)組碼并無二緻。其實如果現有的分(fēn)組碼可以被稀疏矩陣所表達,那麽用于碼的叠代譯碼算法也可以成功的移植到它身上。然而,一(yī)般來說,爲現有的分(fēn)組碼找到一(yī)個稀疏矩陣并不實際。不同的是,碼的設計是以構造一(yī)個校驗矩陣開(kāi)始的,然後才通過它确定一(yī)個生(shēng)成矩陣進行後續編碼。而LDPC的編碼就是本文所要讨論的主體(tǐ)内容。對于LDPC碼而言,校驗矩陣的選取十分(fēn)關鍵,不僅影響LDPC碼的糾錯性能力,也影響LDPC編譯碼的複雜(zá)度及硬件實現的複雜(zá)度。準循環 LDPC 碼(Quasi-Cycle,QC-LDPC)是 LDPC 碼中(zhōng)重要的一(yī)類,是指一(yī)個碼字以右移或左移固定位數的符号位得到的仍是一(yī)個碼字。QC-LDPC 碼的校驗矩陣是由循環子矩陣的陣列組成,相對于其他類型的 LDPC 碼,在編碼和解碼的硬件實現上具有許多優點。編碼可以通過反饋移位寄存器有效實現,采用串行算法,編碼的複雜(zá)度與校驗比特位數成正比,而采用并行算法,編碼複雜(zá)度與碼字長度成正比。對硬件解碼實現,準循環的結構簡化了消息傳遞的路徑,可以部分(fēn)并行解碼,實現了解碼複雜(zá)度和速率的折中(zhōng)。這些優點,使得 QC-LDPC 碼作爲未來通信和存儲系統應用的主要 LDPC 碼。
譯碼算法的選擇
譯碼方法是LDPC碼與經典的分(fēn)組碼之間的最大(dà)區别。經典的分(fēn)組碼一(yī)般是用ML類的譯碼算法進行譯碼的,所以它們一(yī)般碼長較小(xiǎo),并通過代數設計以減低譯碼工(gōng)作的複雜(zá)度。但是LDPC碼碼長較長,并通過其校驗矩陣H的圖像表達而進行叠代譯碼,所以它的設計以校驗矩陣的特性爲核心考慮之一(yī)。由于 LDPC 碼校驗矩陣的稀疏性,其譯碼複雜(zá)度與碼長不是指數關系,而是線性關系,因而 LDPC 碼的碼長可以很長,可以達到幾千到幾萬甚至更高,這樣帶來的一(yī)個好處是:一(yī)個碼字内各比特之間的關聯長度比較長,一(yī)般通過叠代譯碼方法進行譯碼,充分(fēn)利用碼字内各比特的關聯性以提高譯碼準确度,并且還充分(fēn)利用了信道的特征。本課題采用的譯碼算法爲置信傳播(BP)譯碼算法,置信傳播算法是基于 Tanner 圖的叠代譯碼算法。在叠代過程中(zhōng),可靠性信息,即“消息”通過 Tanner圖上的邊在變量節點和校驗節點中(zhōng)來回傳遞,經多次叠代後趨于穩定值,然後據此進行最佳判決,BP譯碼算法有着非常好譯碼性能。
Tanner圖
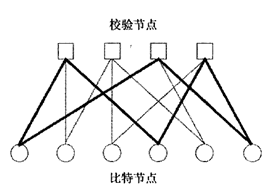
LDPC碼常常通過圖來表示,而Tanner圖所表示的其實是LDPC碼的校驗矩陣。Tanner圖包含兩類頂點:n個碼字比特頂點(稱爲比特節點),分(fēn)别與校驗矩陣的各列相對應和m個校驗方程頂點(稱爲校驗節點),分(fēn)别與校驗矩陣的各行對應。校驗矩陣的每行代表一(yī)個校驗方程,每列代表一(yī)個碼字比特。所以,如果一(yī)個碼字比特包含在相應的校驗方程中(zhōng),那麽就用一(yī)條連線将所涉及的比特節點和校驗節點連起來,所以Tanner圖中(zhōng)的連線數與校驗矩陣中(zhōng)的1的個數相同。以下(xià)圖是矩陣的Tanner圖,其中(zhōng)比特節點用圓形節點表示,校驗節點用方形節點表示,加黑線顯示的是一(yī)個6循環:

Tanner圖中(zhōng)的循環是由圖中(zhōng)的一(yī)群相互連接在一(yī)起的頂點所組成的,循環以這群頂點中(zhōng)的一(yī)個同時作爲起點和終點,且隻經過每個頂點一(yī)次。循環的長度定義爲它所包含的連線的數量,而圖形的圍長,也可叫做圖形的尺寸,定義爲圖中(zhōng)最小(xiǎo)的循環長度。如上圖中(zhōng),圖形的尺寸,即圍長爲6,如加黑線所示。
LDPC編碼
基于校驗矩陣H直接編碼方案
首先推導出根據校驗矩陣直接編碼的等式。将尺寸爲(m,n)校驗矩陣寫成如下(xià)形式:
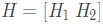
其中(zhōng)H1的大(dà)小(xiǎo)爲m ∗ k ,H2 的大(dà)小(xiǎo)爲m ∗ m 。設編碼後的碼字行向量爲c,它的長度爲n,把它寫成如下(xià)形式
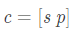
其中(zhōng)s是信息碼的行向量,長度爲k,p爲檢驗行向量,長度爲m,根據校驗公式
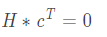
上式展開(kāi)得
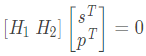
展開(kāi)該矩陣方程,并考慮到運算是在GF(2)中(zhōng)進行的,得到
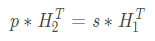
如果校驗矩陣H是非奇異的,則滿秩,所以有
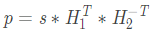
這樣就把碼字的校驗位計算出來了,這種方法需要保證H2 是可逆的,而準循環LDPC碼因其結構化的特點可以保證這一(yī)條件。
基于生(shēng)成矩陣G的編碼方案
令LDPC碼的校驗矩陣H分(fēn)爲兩部分(fēn):
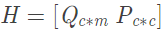
其中(zhōng)子矩陣P的大(dà)小(xiǎo)爲c×c,Q的大(dà)小(xiǎo)爲c×m。計算
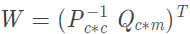
其中(zhōng)的矩陣運算爲模二運算。求得的m×c矩陣W必定是一(yī)個稠密的準循環結構矩陣。由稠密的準循環結構矩陣W可以求得生(shēng)成矩陣:
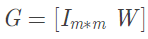
其中(zhōng)I是m×m的單位矩陣。可以看出生(shēng)成矩陣具有準循環結構特性。得到生(shēng)成矩陣G後将碼字X與其相乘C=X*G,獲得編碼後的碼字C。這裏的乘法要滿足有限域的乘法法則。
LDPC譯碼
Gallager 在描述 LDPC 碼的時候,分(fēn)别提出了硬判決譯碼算法和軟判決譯碼算法兩種。經過不斷發展,如今的硬判決算法已在 Gallager 算法基礎上進展很多,包含許多種加權比特翻轉譯碼算法及其改進形式。硬判決和軟判決各有優劣,可以适用于不同的應用場合。
比特翻轉算法(BF)
硬判決譯碼算法最早是 Gallager 在提出 LDPC 碼軟判決算法時的一(yī)種補充。硬判決譯碼的基本假設是當校驗方程不成立時,說明此時必定有比特位發生(shēng)了錯誤,而所有可能發生(shēng)錯誤的比特中(zhōng)不滿足校驗方程個數最多的比特發生(shēng)錯誤的概率最大(dà)。在每次叠代時均翻轉發生(shēng)錯誤概率最大(dà)的比特并用更新之後的碼字重新進行譯碼。具體(tǐ)步驟如下(xià):
設置初始叠代次數 k1及其上限kmax 。對獲得的碼字y=(y1,y2…yn)按照下(xià)式展開(kāi)二元硬判決得到接收碼字的硬判決序列Zn 。
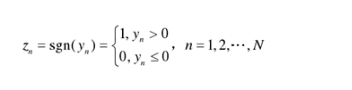
若k1=kmax ,則譯碼結束。不然,計算伴随式s=(s0,s1,…sm-1),sm表示第m個校驗方程的值。若伴随式的值均爲 0,說明碼字正确,譯碼成功。否則說明有比特位錯誤。繼續進行步驟3。
對每個比特,統計其不符合校驗方程的數量fn (1<=n<=N)
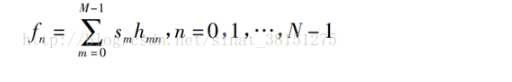
4. 将最大(dà)fn 所對應的比特進行翻轉,然後k=k+1,返回步驟2。
BF 算法的理論假設是若某個比特不滿足校驗方程的個數最多,則此比特是最有可能出錯的比特,因此,選擇這個比特進行翻轉。BF 算法舍棄了每個比特位的可靠度信息,單純的對碼字進行硬判決,理論最爲簡單,實現起來最容易,但是性能也最差。當連續兩次叠代翻轉函數判斷同一(yī)個比特位爲最易出錯的比特時,BF 算法會陷入死循環,大(dà)大(dà)降低了譯碼性能。
置信傳播算法(BP)
置信傳播(Belief Propagation)譯碼算法是消息傳遞(Message Passing)算法在 LDPC譯碼中(zhōng)的運用。消息傳遞算法是一(yī)個算法類,最初運用于人工(gōng)智能領域,人們将其運用到 LDPC 碼的譯碼算法中(zhōng),提出了LDPC 碼的置信傳播算法。置信傳播算法是基于 Tanner 圖的叠代譯碼算法。在叠代過程中(zhōng),可靠性信息,即“消息”通過 Tanner圖上的邊在變量節點和校驗節點中(zhōng)來回傳遞,經多次叠代後趨于穩定值,然後據此進行最佳判決。
在介紹BP譯碼算法之前需要先了解一(yī)下(xià)Tanner圖的概念。
Tanner圖是一(yī)種表示LDPC碼的雙向圖,圖的下(xià)面每個節點表示碼字的一(yī)個比特位,稱比特節點(bit nodes)。上面每個節點稱爲校驗節點(check nodes)。校驗矩陣中(zhōng)爲1的元素,表示Tanner圖中(zhōng)比特節點和校驗節點之間存在連接邊,這條邊可稱爲兩端節點的相鄰邊,相鄰邊兩端的節點稱爲相鄰節點,每個節點相鄰邊數稱爲該節點的度數。Tanner圖是用來描述LDPC碼結構的有效工(gōng)具,同時也是叠代譯碼算法的參考工(gōng)具。在Tanner圖中(zhōng)校驗節點和變量節點之間可以進行消息的可靠傳遞,首先變量節點接收初始化後驗概率進行計算,将得到的可靠信息傳遞給相鄰的校驗節點;經過校驗節點更新算法的計算,再将得到的運算結果傳回至與其相鄰的變量節點處,随後變量節點再将由校驗節點得到的可靠信息以及初始化後驗概率信息進行處理;将最後得到的有效信息進行判決得到譯碼結果。
LDPC碼的譯碼較爲複雜(zá),下(xià)面以置信傳播算法舉一(yī)個簡單的例子來說明一(yī)下(xià)。
發送碼字C=(C9,C8,C7,C6,C5,C4,C3,C2,C1),其監督矩陣H是

則C必然滿足線性方程組HCT = 0 ,即
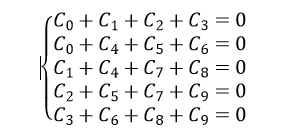
通過信道後接收到的碼字Y=(Y0,Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9)可能包含錯誤,因此伴随式S= HYT ≠ 0 。将此線性方程組用如圖所示的Tanner圖來表示。

圖中(zhōng)的X0,X1…X9稱爲變量節點,代表10個比特C0,C1,C2…C9,它們是譯碼器待求解的未知(zhī)變量。圖中(zhōng)的□成爲校驗節點,代表線性方程組中(zhōng)的每一(yī)個校驗方程,連線就代表方程中(zhōng)此變量的系數爲1。
譯碼過程是在變量節點和校驗節點之間傳遞信息。每個變量節點告訴它所連接的校驗節點“我(wǒ)認爲該變量是什麽”,而校驗節點告訴它所連接的變量節點“我(wǒ)認爲該變量應該是什麽”。經過反複的消息傳遞後,變量節點和校驗節點不斷改變自己對各個變量是什麽的看法,最終能形成一(yī)個滿足校驗方程的碼字,這就是譯碼的結果。如果經過充分(fēn)的叠代後仍然不能形成一(yī)個滿足校驗方程的碼字,則譯碼器宣布它無法譯出這個碼字,即譯碼失敗。
置信傳播譯碼算法的基本流程如下(xià):
在叠代前,譯碼器接收到信道傳送過來的實值序列y=(y1,y2,….yn),所有變量節點bi接收到對應的接收值yi。
第一(yī)次叠代:每個變量節點給所有與之相鄰的校驗節點傳送一(yī)個可靠性消息,這個可靠性消息就是信道傳送過來的值;每個校驗節點接收到變量節點傳送過來的可靠性消息之後,進行處理,然後返回一(yī)個新的可靠性信息給與之相鄰的變量節點,這樣就完成了第一(yī)次叠代;此時可以進行判決,如果滿足校驗方程,則不需要再叠代,直接輸出判決結果,否則進行第二次叠代。
第二次叠代:每個變量節點處理第一(yī)次叠代完成時校驗節點傳送過來的可靠性消息,處理完成後新的消息發送給校驗節點,同理,校驗節點處理完後返回給變量節點,這樣就完成了第二次叠代。完成後同樣進行判決,如果滿足校驗方程則結束譯碼,否則如此反複多次叠代,每次都進行判決,直到達到設定的最大(dà)叠代次數,譯碼失敗。在每次叠代過程中(zhōng),無論是變量節點傳送給校驗節點的信息或者校驗節點傳送給變量節點的信息,都不應該包括前次叠代中(zhōng)接收方發送給發送方的信息,這樣是爲了保證發送的信息與接收節點已得到的信息相互對立。
假設在 AWGN 信道中(zhōng),信道編碼後的碼字C=(c1,c2,…,cn)通過調制映射爲調制序列X=(x1,x2…,xn),然後經信道傳輸,接收的序列爲y=(y1,y2…,yn)。
爲後面章節的推導方便,先介紹一(yī)引理。
引理:
一(yī)個獨立的比特序列,其長度爲m,假設第i個比特爲 1 的概率爲pi ,則整個序列中(zhōng)出現偶數個1的概率爲
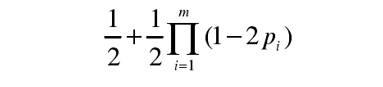
出現奇數個 1 的概率爲
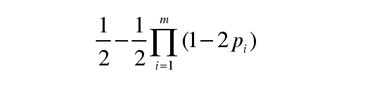
這是信道編碼領域中(zhōng)經常使用的一(yī)個定理,故直接使用。
Gallager 定理:對于(n,j,k)規則 LDPC 碼,Pil 第i個校驗方程中(zhōng)第 l 校特爲1的概率,則
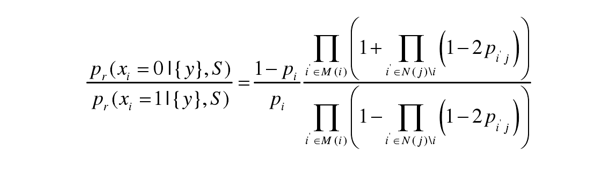
其中(zhōng):
Pr (xi =0∣{y},S)表示在程組爲S ,接收序列爲y的條件下(xià)判斷發送幀中(zhōng)的第i個比特爲0的概率
Pr(xi =1∣{y},S)表示在程組爲S,接收序列爲 y的條件下(xià)判斷發送幀中(zhōng)的第i個比特爲0的概率
pi 表示發送序列的第 i位爲1的先驗概率;
M(i) 表示校驗節點的集合,集合中(zhōng)的節點均與變量節點i相鄰;
N(j) 表示變量節點的集合,集合中(zhōng)的節點均與校驗節點 j相鄰。
由上節介紹的 BP 算法的原理及 Gallager 定理中(zhōng)的描述可知(zhī),變量節點i傳遞給校驗節點j的可靠性信息q{ij}(1)就是Pr(Xj=1|{y},S),于是定義
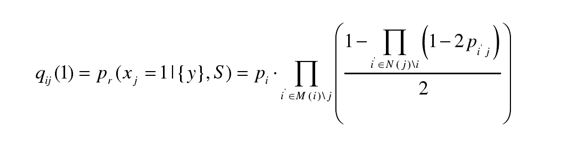
表示變量節點i ii傳遞給校驗節點j 的外(wài)部概率信息,即在得到除校驗節點j以外(wài)的其他所有校驗比特和信道的外(wài)部信息後,判斷變量節點ci =1的概率。
再定義
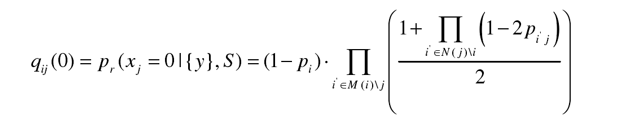
表示變量節點i傳遞給校驗節點 j 的外(wài)部概率信息,即在得到除j 以外(wài)的其他所有校驗比特和信道的外(wài)部信息後,判斷變量節點ci =0的概率。
另一(yī)方面,校驗節點 j傳遞給變量節點i的可靠性信息應該爲在給定信息位和其他信息位具有獨立概率分(fēn)布條件下(xià),校驗方程 j滿足的概率。将此可靠性信息記爲rji ,則
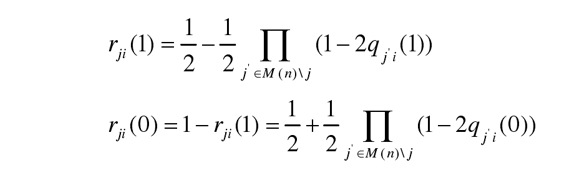
将上式代入
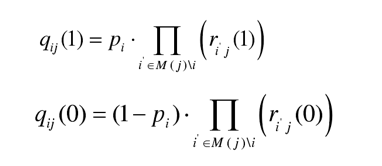
根據以上的描述和符号定義,概率 BP 譯碼算法流程可以歸納爲如下(xià)幾個步驟:
(1) 初始化
計算經信道傳輸後各變量節點的初始概率pi(1)和pi (0)。然後對每個變量節點求傳遞給與其相鄰的校驗節點的可靠性信息
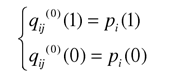
其中(zhōng)的上标(0)表示叠代次數。
2) 校驗節點處理過程(rij 的計算)
求出第l ll次叠代過程中(zhōng)校驗節點i遞給與之相鄰的變量節點j可靠性信息
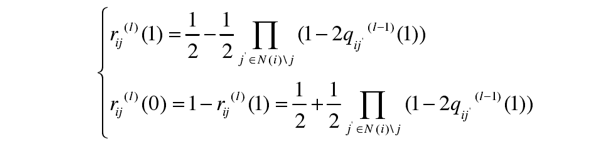
其中(zhōng)的上标(l)和(l−1)均表示叠代次數。
(3)變量節點處理過程(qij 的計算)
求出第l 次叠代過程中(zhōng)變量節點j傳遞給與之相鄰的校驗節點i ii的可靠性信息
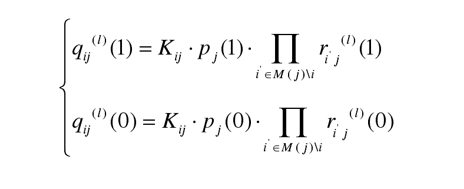
其中(zhōng)的Kij 是校正因子,使每次計算出的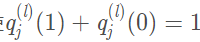
(4)譯碼判決
在本次叠代過程處理最後,重新計算各變量節點的可靠性信息
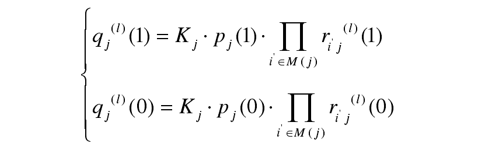
其中(zhōng)的 Kj 也爲校正因子,目的是使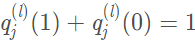
如果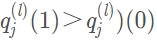 ,那麽這一(yī)點的估計值時ci=1,否則估計值爲ci= 0。如果估計值滿足奇偶校驗方程,那麽終止算法,否則算法繼續運行,直到達到預先設置的最大(dà)叠代次數。
,那麽這一(yī)點的估計值時ci=1,否則估計值爲ci= 0。如果估計值滿足奇偶校驗方程,那麽終止算法,否則算法繼續運行,直到達到預先設置的最大(dà)叠代次數。
仿真驗證
| LDPC碼 | 基于IEEE 802.16e标準 |
| 碼長 | 1440 |
| 碼率 | 1/2 |
| 有限域 | 四元 |
| 叠代次數 | 20 |
| 調制方式 | QPSK |
| 單一(yī)信噪比下(xià)仿真次數 | 10^5 |
| 最小(xiǎo)誤碼總數 | 不少于200 |
| 信道 | 高斯信道 |
仿真說明如下(xià):
下(xià)圖是在高斯信道下(xià),碼字經過LDPC編碼和未編碼的譯碼結果對比圖,爲了保證對比的有效性,仿真中(zhōng)LDPC碼與未編碼的碼字等長,同爲1440,LDPC碼通過BP譯碼算法譯碼,而未編碼的碼字通過解調硬判決譯碼。

仿真結果分(fēn)析:從圖可以看出碼字經過LDPC編譯碼之後其抵抗噪聲的能力極大(dà)加強,與未編碼的碼字相比,在誤碼率都爲1e-4時,其性能提高了9.5dB左右,從而驗證了LDPC碼是一(yī)種性能極佳的信道糾錯碼。
結束語
目前LDPC碼研究領域的主要工(gōng)作集中(zhōng)在譯碼算法的性能分(fēn)析、編碼方法、碼的優化算法等,經過研究人員(yuán)的努力,LDPC碼的研究取得很大(dà)進展,但仍有許多問題需要進一(yī)步研究:
(1)LDPC碼校驗矩陣的構造,盡管在構造最優的LDPC碼方面取得了一(yī)些進步,但目前還沒有一(yī)套系統的辦法來構造所需要的好碼,特别是在碼字長度有限、碼率一(yī)定的條件下(xià),構造性能優異的好碼是一(yī)個非常具有挑戰性的課題。
(2)LDPC編碼系統的聯合優化設計,将編碼技術與調制技術、均衡技術、時空編碼技術、OFDM技術結合進行性能優化是當前及将來的發展方向之一(yī)。
(3)無線衰落信道及MIMO技術下(xià)LDPC碼的性能分(fēn)析方法及優化設計準則。目前LDPC碼字的優化設計主要在加性高斯白(bái)噪聲信道下(xià)得到的,而無線衰落信道下(xià),特别是時變信道非線性環境下(xià)碼字的性能分(fēn)析方法、優化設計準則和信道估計的影響也是非常關鍵的課題,需要進一(yī)步的研究探索。
此外(wài),基于LDPC碼的鏈路自适應技術,LDPC碼在集成通信網物(wù)理層、應用層聯合優化系統中(zhōng)的應用,LDPC碼在無線局域網和深空宇航中(zhōng)的應用,基于LDPC碼的圖像傳輸、圖像數字水印系統中(zhōng)的應用以及尋找更适合硬件實現的LDPC碼編譯碼方法等都是非常值得研究的課題。
其他學院知(zhī)識

科楠公衆号